とある組合せ論の命題の母関数を用いた証明
これは鯵坂もっちょさん企画のアドベントカレンダーの記事です。
私がブログを更新するのはほぼ一年ぶりで、最後に書いたのは昨年の素数大富豪アドベントカレンダーの記事でした。素数大富豪の日である12月13日に札幌で素数大富豪に興じていたのが約一年前。そう考えると2018年はあっという間でした。
今回の話題は、昨年の今頃に私が修論で書いていた内容の一部です。
※体裁修正中につきPC推奨
都合によりちょっとガロアなので(=時間がないので)*1、分割数と母関数の知識等を仮定して進めます。
まず、整数の分割を扱いやすくするため、非負整数の分割全体と一対一に対応する集合
を用意しておきます。一対一の対応は、の各元(非負整数列)
を、正整数
をちょうど
個成分に持つような分割に対応させることで得られます。
たとえばのときは次のようになっています。...
(いずれも第5項以降は0)
いきなり分かりにくい内容かもしれません。「分割数を扱いやすい形で表した」という認識だけでもOKです。
本題に入りましょう。次の問題を考えます。
非負整数に対して
を計算せよ.
再びn=4を例に計算してみます。前述のとおりの元は以下の5つです。
これら5つの数列(分割)のそれぞれについて、無限積を計算します。ただし無限積といっても、数列の0の項は無限積において1を掛けることに対応するので考えなくてよく、実質いくつかの分数の掛け算をするだけになります。
最後にこの総和を計算します。
よって、と計算できました。
5つの分数を足したらぴったり1になったわけですが、勘のいい方はお気づきのとおり、これは偶然ではありません。というわけで、次の命題を示します。
任意のに対して
\begin{equation}
T(n):=\sum_{\{ u_i\} \in U(n)} \prod_{i=1}^{\infty} \frac{1}{i^{u_i} \cdot u_i !} =1
\end{equation}
が成り立つ.
私は修論研究の過程で、この事実を今から紹介する証明とともに発見しました。とはいえ適当な本を漁れば書いてあるような初等的な事実のような気もします(実際、研究中に複数の方から群論の知識を用いて比較的簡単に証明できる旨の指摘を受けました)。以下の証明に簡潔さや明快さはあまりありませんが、これこそが「私の好きな証明」です。

数学の証明を山登りに例えるなら、この証明は「あまり見慣れない登山口から入り、途中もそれほど良い眺望はないけれど、最後に一気に視界が開けて頂上から美しい景色が見える」タイプだと思います。
以上、体裁の整っていない分かりにくい記事にお付き合いくださりありがとうございました。そのうち修正します。。
*1:タカタ先生の漫才より引用
やたらすごい素数と合成数in札幌
2
3
5
7
11
13
17
19
23
29
31
41
47
59
61
67
71
73
83
89
97
101
103
107
109
127
139
151
211
227
229
311
421
443
449
487
499
523
541
569
587
613
641
643
691
743
751
811
821
823
853
863
887
911
967
977
983
1009
1013
1021
1069
1087
1103
1117
1213
1231
1487
1489
2213
2221
2339
3109
4111
4513
4567
5101
5659
6101
6421
6427
6581
7129
8123
8513
8627
8861
8863
9013
9103
9127
9439
9511
9973
10007
10103
10459
12101
12109
12112
12113
12119
12613
12911
13109
13121
21011
21013
21211
24611
25253
29723
41011
41113
41213
46237
47653
61211
61463
65111
66107
69593
71011
81013
81019
81041
81043
84211
86117
86131
88817
95111
105863
108107
109841
109843
111211
121013
121157
131011
131111
131213
131311
291113
412127
451013
461011
551489
612109
612611
662443
668611
681011
1010419
1031593
1210873
1211593
1212121
1212851
1213241
1249111
1381297
2102383
2136139
3111013
4101313
4510711
5101211
5121211
5131211
6661111
7111213
8121011
8121013
8810101
8871113
9121213
9131011
11524831
12131113
12581089
12661213
13111013
13111211
13410829
35121211
55836971
77161213
81217121
84711223
85451071
93174881
111664811
121212127
862410121
1213121311
3512121211
4510131013
8897101013
9101112131
9876543211
6=2*3
8=2*2*2
9=3^2
10=2*5
12=2*2*3
14=2*7
25=5^2
51=3^17
64=2^6
84=2^2*3*7
86=2*43
91=7*13
106=2*53
123=3*41
124=2*2*31
125=5^3
169=13^2
171=3^2*19
511=7*73
711=3*3*79
729=3^6
910=2*5*7*13
913=11*83
1010=2*5*101
1024=2^10
1110=2*3*5*37
1211=7*173
1310=2*5*131
1312=2^5*41
1313=13*101
1369=37^2
1849=43^2
2209=47^2
78125=5^6*5
121300=2*2*5*5*1213
これは何の変哲もない只の200種類の素数と35種類の合成数に見えたかもしれない。
本当にそうだろうか?
なんと、これらはすべて、先日の「素数大富豪in札幌」で実際に出された数なのである。
こんにちは。みうらです。
今日書いているのは、素数大富豪アドベントカレンダー2017の16日目の記事です。
インテジャーズのアドベントカレンダー
に参加できなかった(話題と時間がなかった)ためちょっとだけパロディをしています*1。
さて、私は今週の水曜日(12/13=素数大富豪の日)に素数大富豪in札幌に初めて参加してきました。冒頭の200種類の素数および35種類の合成数は他の方にも協力いただいて記録したものです*2。T、J、Q、Kの表記は数に直したので何枚出しか分からないものもありますがご了承ください。
まずは素数のほうから観察していきましょう。
・出されなかった100以下の素数は4種類
37
43
53
79
は、記録されませんでした。37と79はそれぞれ上位互換の73、97があるため自然ですが、43と53は意外でした。
しかしこれはどちらも3のつく素数で、3は人名の語呂合わせでよく使うので納得です。特に53はコックさん(593)や婿さん(653)関連の素数で必要な5と3からなるため出されなかったのでしょう。
・3桁、4桁、5桁がほぼ同数
桁数ごとに分類すると
一桁:4種類
二桁:17種類
三桁:36種類
四桁:36種類
五桁:38種類
六桁:21種類
七桁:25種類
八桁:14種類
九桁:3種類
十桁:6種類
となっています。二、三桁の素数に比べ四、五桁は使われるものの割合は少ないですが、桁数を決めたときの素数の個数は大きな桁になるほど増えていきます(素数の減少スピードは対数オーダーであり指数オーダーほどではない)ので母数が大きく、三から五桁はちょうどそのバランスが取れているみたいです。
・最高桁が3のものが極端に少ない
やはり、偶数消費型の割合が高いですね。7や9から始まるものは(数を大きくできるため)しばしば出されますが、3からのものははたったの7種類です。人名素数の影響もあるでしょう。
なお、最高桁が1のものはほとんどが絵札から始まるものです。
合成数のほうも見てみましょう。
・難度の高い出し方が多い
指数表記をうまく利用した合成数出しがとても多かったです。また絵札を含む合成数は一部を除き出しにくいものばかりですが、素因数が手札に揃ったチャンスを見逃さずに出しているようですね。すごいですね。
・2は便利
2のべき乗や2*5を含む合成数、そして素数の2乗(1369=37^2など)で2が使われています。奇数の2乗は十の位が必ず偶数なので(証明は読者への宿題とする)、これらはすべて偶数を2枚以上消費できる出し方です。
今見てきたように、素数、合成数ともに使われる数に傾向はあります。これらをもっと研究すると戦略も見えてくるかもしれません。
しかし、たったの7時間でこれだけの数が登場しているのはそれだけでも驚きですし、定石の作戦や定番の素数にとらわれない自由な発想で素数大富豪を楽しんでいることに感激しました。素数の前では人はみな平等、という言葉を思い出しました*3。
いやあ、素数っていいですね。眺めていると本当に落ち着きます。
合成数も、美しい素因数分解を見ていると心が癒されます。
というか冒頭で一気に書き並べたのは自分で鑑賞するためだったりもします。
人に元気を与えたり楽しませたりする、本当に「やたらすごい」素数と合成数です。
実は私は今週の初め、大事な試験で失敗してかなり落ち込んでいたのですが、たくさんの素数と合成数、そして素数大富豪愛好家の方々に元気をもらいました。それだけで、はるばる東京から参加して良かったと思えます。二世さん、参加者のみなさん、ありがとうございました。
それでは今日はこの辺で。
明日はキグロさんの記事です!
人名で覚える四つ子素数
みなさんこんにちは。9月が終わりますね。
9月に31日はないのでまたギリギリの投稿です。
さて、いよいよMATH POWERが一週間後に迫ってきました。私は別の用で1日目の夜から2日目の朝までしか会場にいられないのですが、今年も素数大富豪を楽しみたいと思います。また勝ちたいなあ。
本記事では、素数大富豪で非常に便利な四つ子素数を人の名前で覚える語呂合わせを紹介していきます。二枚出しから四枚出しまでの14種類です。
以下、語呂合わせはすべて「〜さん」の形で掲載しますが、この「さん=3」を1,7,9に変えても素数ということです。
103…父さん
二枚出し3桁唯一の四つ子。超シンプルな語呂合わせ。基本中の基本。
193…一休さん
覚えやすいけど、193以外は911,971,991など上位互換が存在し需要は高くない。革命時には重宝するか?
823…羽生さん
フィギュアじゃなくて、将棋のほう。というか正直ここまでは語呂合わせなしで覚えている方がほとんど。
偶数消費型なので超便利。
さあ、本題はここから。
1483…石破さん
政治家でしょうか、いいえ、ラマヌジャンの天敵です。1729より小さい四枚出し(つまり革命直後に出せる)唯一の四つ子。これだけで戦略の幅が広がる。
1873…岩名さん
今回は人名ということなので、岩魚ではない。こだわる意味ないけど。
岩波と覚えるのが普通かも。
3253…みつこさん
下の名前が登場。それ以上特に言うことがない。
3463…三四郎さん
みつこさんとセットで覚えたい素数。三、四が漢数字そのままなのでとてもわかりやすい。
4,6が消費できる。
5653…ゴロゴさん
謎の人物。間違える恐れがなければゴルゴって言ってもいい。
私が高校の頃、古文単語を565個覚える『古文単語ゴロゴ』というのが話題になった。今も新版が出ているようで。
9433…櫛見さん
四枚出し4桁の最大四つ子。「苦しみ」という覚え方は心が苦しくなるのでやめておく。
21013…太井さん
以前は「ふと遺産」(振り返ってみたら世界遺産があった的な)で覚えていたけどこの際人にしちゃえ。
21011と21013は三枚出しとして頻出。
51343…こけしさん
「け」=K=13ということ。人をあきらめた結果がこれ。それっぽいので許してほしい。
81043…八頭身さん
偶数消費型で四枚出し5桁なのでめっちゃ使える。
詳しくないけどこういうのがある(いる)ようで。
⊂_ヽ、
.\\ Λ_Λ
\ ( ´Д`)
. > ⌒ヽ
/ へ \
/ / \\
レ ノ ヽ_つ
/ /
/ /|
( ( 、
| |、 \
. | / \ ⌒l
| | ) /
ノ ) し'
(_/
99133…九九艦さん
人の語呂合わせが全然思いつかない中、九九式艦爆なるものを発見。艦これでも登場するみたいなので人ってことにしよう。
101113…遠い爺さん
10 1 J 3の意味。遠く離れた故郷にお爺さんが住んでる設定。
以上14種類、いかがでしたでしょうか。四つ子素数はコスパ最強で、自明な李さん(11~19)を含めれば15×4=60個もの素数を一気に覚えられることになります。簡単でしょ?
それでは今日はこの辺で。お会いする方はMATH POWERでお会いしましょう。
電卓で遊ぼう! ~途中で止まるカウントダウン~
みなさんこんばんは。今日は8月31日です。
明日から2学期が始まる小中学生などは、今ごろ宿題に追われているかもしれません。
しかし私にも実は、今日までにやろうと思っていたことがありました。それはまさに、このブログの更新です。
8月31日。「毎月1記事」にギリギリ間に合った今回のテーマは、次の動画の解説です。
twitter.comカウントダウン#電卓 pic.twitter.com/2EVyDLYuSb
— みうら@素数大富豪 (@miura_prime) 2017年7月26日
電卓に表示されている数がイコールキーを押すたびに小さくなっていきますが、3になったところで動かなくなります。これのタネ明かしです。
さて、電卓といえば、最近キグロさんがニコニコ動画に「電卓の使い方講座」を投稿しています。
実は、このPart2で紹介されている「ラウンド・小数点セレクター」と「定数計算」を使うと、3で止まるカウントダウンが実現できるのです。
事前準備①:ラウンドセレクターを四捨五入、小数点セレクターを「0」にする
これにより、計算結果の小数第一位を四捨五入して整数にする設定ができたことになります。
例えば、
と表示されます。
事前準備②:定数計算で0.87倍を繰り返せるようにする
「0.87××」と押すと、イコールを押すたびに、表示されている数の0.87倍の計算をしてくれます。①と組み合わせると、
のようになります。
あとは、11と入力して、イコールを押していくだけです。
このように、11から4までの整数は、0.87倍して小数第一位をを四捨五入すると1小さい整数になります。しかし
なので、3の0.87倍の小数第一位を四捨五入すると3のまま。何度イコールを押しても、3は変わらないのです。
なお動画では、画面に「GT」という表示が最初から出ているようにするために(数以外の表示が終始変わらないように)、一度計算をして10になったところからカウントダウンを始めています。
このように、電卓の諸機能をうまく使うと一見不可解な計算や動作を実現することができます。今回のカウントダウンの他にも、
となる素数カウントダウンも工夫すると実現できるので、ぜひ考えてみてください。
三角形の合同2分割
一か月半以上空いてしまいました。前回「もっと書かなきゃ」と言ったにもかかわらず、です。
とりあえず目標を下方修正して、まずは最低ひと月1記事を書きたいと思います。
さて、今回のテーマは、今月初めに開催されたロマンティック数学ナイトでの三好さんのプレゼン「図形パズル 双子カバリング問題の深淵」に関係するものです。
辺の比がである直角三角形の「双子カバリング」のはみ出し率の記録更新物語が非常に熱かったプレゼンでしたが、この問題を考える上で
そもそも、辺の比がである直角三角形は合同な2つの図形に分割できないのか?
という問いはとても大切です(もし合同2分割可能なら、はみ出し率が0パーセントになるため)。ロマ数の一か月前くらいに「みらいけん数学デー」にて私は三好さんらとこの問題を考え始め、その翌日くらいに「合同2分割できない」ことが証明できたので、以下、それを解説することにします。
というわけで、今日は次の命題を証明します。
命題:3辺の長さがすべて異なる三角形は合同2分割できない
ただし、ここでの合同2分割とは、”周長や頂点の数が有限である”2つの合同な図形に分割することを意味するものとします(フラクタル等は除いておきます)。
【証明】
背理法により、多角形による合同2分割の不可能性を示す。曲線を含む図形を考える場合は、直線部にだけ着目して同じ議論をすればよい。
3辺の長さがすべて異なる三角形が多角形により合同2分割できたと仮定し、分割の線が本の線分からなるとする。このとき、分割線は次の図に示す6つのパターンのどれかである。

しかし、分けられた2図形は合同なので、特に辺の本数は一致していなければならない。①の2図形は辺の数がそれぞれと
なので不適。同様に、②、③、⑤、⑥についても辺の数が一致していないことがわかる。したがって④の場合しかありえない。
④の場合について、図のように、分割線の各線分の長さを(頂点の側から)とし、分割線と頂点を共有する2辺をそれぞれ
、また分割線で分けられた三角形の辺の長さを(
の側が合うように)
とおく。

二つの図形の辺の数はともにだが、合同であるためには、この
本の辺の長さ(構成)がすべて一致していなければならない。すなわち、
と
が”数の並べ替え”になっていなければならない(集合として一致しているかではなく、同じ数も別々に数えたうえで構成が一致しているかどうかに着目する)。
しかし、が双方に共通しているため、結局これを除いた
が数の並べ替えになっていなければならない(どの辺とどの辺が対応するか、については議論していないことに注意)。
つまり、
または
の場合しかありえないことになるが、前者の場合は元の三角形が二等辺三角形になるため矛盾。後者も三角不等式を満たさない(三角形がつぶれてしまう)ため矛盾。
以上で証明が完了しました。実はこれと同じ方法で、
奇数に対して、辺の長さがすべて異なる
角形は合同2分割できない
ことが示せます。
では、偶数角形は…?ぜひ考えてみてください。
パズルと不定方程式 ~立体編~
気づいたら6月になってました。前回の記事が5月7日だったので、ほぼ一か月ぶりの更新です。書きたいテーマはいくつもあるのでもっと書かなきゃなあと思います。
今日のテーマはこれです。現在、神保町のみらい研究所に置かせてもらっているパズルです。

二種類のピース、合計10個を箱に詰めるのが目的。ピース構成は以下のとおりです。
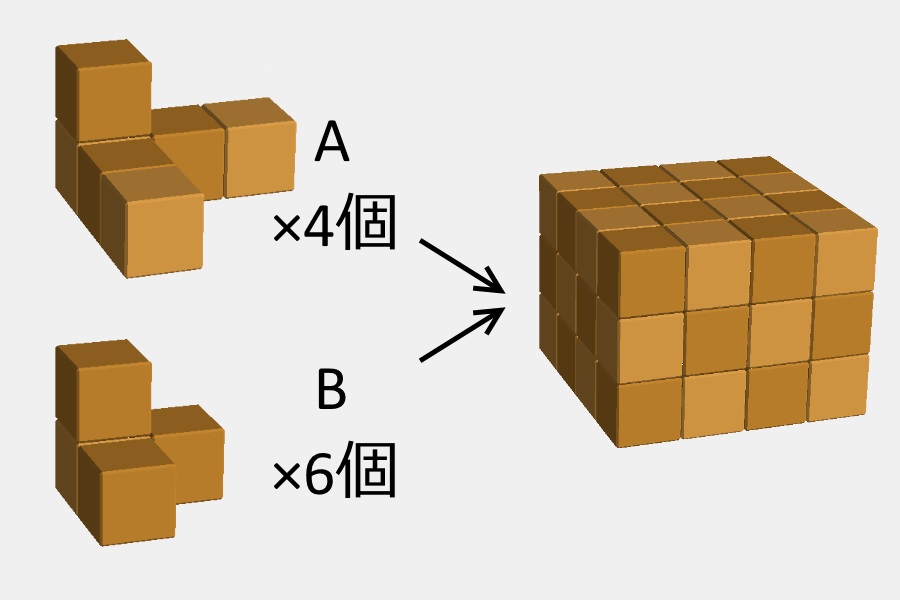
大きい方(以下「ピースA」と呼ぶ)が6単位分、小さい方(以下「ピースB」と呼ぶ)は4単位分のピースで、箱(一合升)は4×4×3=48単位分の直方体です。
なので、体積としてはぴったり。そしてなんと驚くことに、このパズルの解は対称なものを除くとただ一通りなのです(コンピュータで確かめました*1)。
でも、もしかすると、ピースAとピースBのそれぞれの個数を変えれば、この二種類で一合升をぴったり埋める方法が他にもあるかもしれない。今回は不定方程式を使って、この問題を考えていきます。
ピースAを個、ピースBを
個使って一合升を埋めるとすると、
という等式が成立していなければなりません(今は「二種類のピースを使う」ということなので、はともに正の整数とします)。
この不定方程式の解は一通りではないですが、実はある工夫をすると、もっと強い条件を表す方程式を立てることができます。

この図は、各ピースと4×4×3の箱を、隣接する単位立方体が異なる色になるように青と緑で色付けした様子を表しています。一つの形に対して二つの塗り方がありますが、直方体については回転によって同じものだと分かります。
ここで、それぞれの形における青と緑の数を数えてみます。
まず、直方体の箱については当然、青と緑は24個ずつ。ピースAについても、(塗り方は二種類ありますがどちらも)青と緑が3個ずつです。しかしピースBは、「青1個と緑3個」または「青3個と緑1個」になっている。これが重要です。
塗り方の違うピースを別物と考えて、改めて
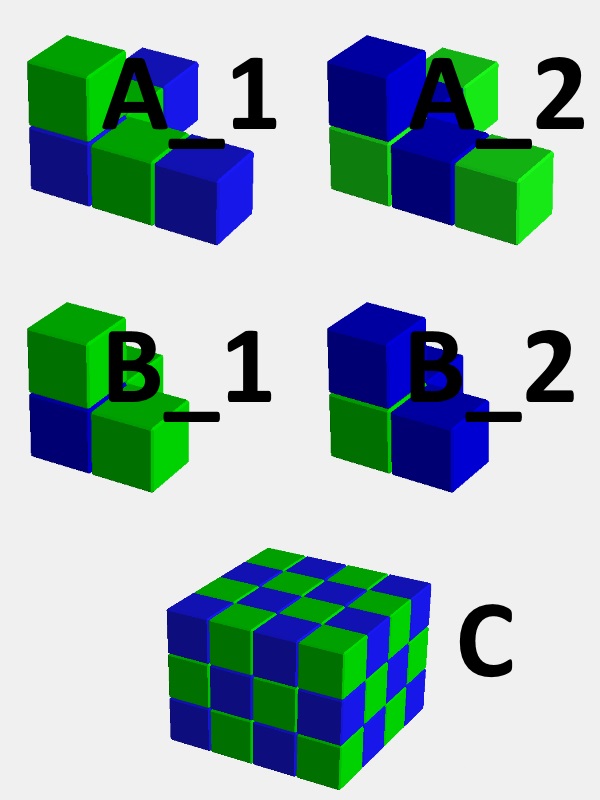
と呼ぶことにしましょう。すると、「AとBの二種類で一合升を埋める」という問題は「A,A
,B
,B
を使って色が合うようにCを作る」という問題に置き換えられます。ただし、後者については「A
とA
は少なくとも一方は使う」「B
とB
は少なくとも一方は使う」という条件付きです。
使われるA,A
,B
,B
の個数をそれぞれ
とおくと、青の立方体の個数について
という式が立ち、さらに緑の立方体の個数について
が成り立つはず。ここでは非負整数で少なくとも一方は正、
も非負整数で少なくとも一方は正です。この不定方程式を解いてみます。
まず、から
が
の倍数であること、そして2式の差から
であることがわかるので、
と書けます(は正整数)。これを
に代入して両辺を
で割ると
が得られ、は正なので
(すなわち
)となります。つまり結局
(ピースBの個数)
が個数の組み合わせとしては唯一で、この二種類で一合升をぴったり埋める方法は他にはないことがわかりました。
なお、式と式
を足し合わせると
となり、これは最初の不定方程式
と同じものです。なので式は、最初の式を「色分けによって精密化した」ものだと考えられます。この色分けの方法は平面だと市松模様と呼ばれる塗り方なので、今回のような議論は「市松理論」と呼ばれることもあるようです。岩澤理論みたいでかっこいいですね!
それでは今日はこの辺で。
*1:BurrToolsというソフトを使っています
人力素数判定をしよう!
みなさんこんにちは。倍数判定の時間です。
素数大富豪をしているとき、あるいは街中で見つけた自然数が素数かどうか気になったとき。私たちが日常生活を送るうえで、倍数判定力(素数判定力)を問われる局面は多々あると思います。今日は私がそのような場面でどのように考え、どのように素数と出会っているかを紹介するため、倍数判定法の記事を書きます。
与えられた自然数nが素数かどうかを人力で判定するとき、√n以下の素数で割ってみる「試し割り」以外に有用な方法はほとんどないでしょう。「素数pで割れるかどうか」は「素数pの倍数かどうか」と同じことなので、実際には素数の倍数判定が重要になってくるわけです。小さい素数から順に、倍数判定法を見ていきましょう。
2,3,5の倍数判定 ~一の位チェック&桁和チェック~
一の位が偶数なら元の数も偶数であり、一の位が5か0なら5の倍数です。また各桁の和が3の倍数なら元の数も3の倍数です。
例:5123874は2の倍数。83025は5の倍数。また5+1+2+3+8+7+4=30と8+3+0+2+5=18は3で割れるので、この二数は3の倍数でもある。
〈追記〉
要は、一の位が1,3,7,9のいずれかでないと2か5で割れてしまいます。
また、3の倍数判定については「桁和が3で割れるか否か」をチェックできればいいので、
・3の倍数の部分が見えたら消す
・等差数列をなす三整数は消す
を使うと早いです。たとえば458881479は、先頭の45と末尾の9を消すと888と147という二つの等差数列が残るので3の倍数です。
7,11,13の倍数判定 ~1001チェック→91&交代和チェック~
7*11*13=1001なので、判定したい自然数nから1001の倍数を引いても、「7の倍数かどうか」「11の倍数かどうか」「13の倍数かどうか」の性質は変わりません。さらにここから7と13の倍数判定については、7*13=91の倍数を引いていって確かめることができます。また、nの偶数桁の和と奇数桁の和との差を計算して11で割れるかどうか確かめれば、nが11の倍数かどうかを確かめたことになります(証明は略)。
例:3157から1001*3=3003を引くと154であり、154から91を引くと63である。63は7では割れて13では割れない。また154の偶数桁は5のみで奇数桁の和は1+4=5であり、5-5=0は11の倍数。よって3157は7と11の倍数であり13の倍数ではない。
7*11*13が1001であることには数の神秘を感じずにはいられません。なお、91を使った倍数判定は今年1月にtsujimotter氏により見出されました。
ここまでは、素数大富豪プレーヤーをはじめとする多くの方がご存知の手法かと思います。本題はここからです。
〈追記〉
特に6桁の数を判定したい場合、「上3桁と下3桁の差を計算する」ことが「1001の倍数を引く」操作になっているので、上3桁と下3桁が近い数のときは1001チェックはとても早く終わります。例えば108109は上下の差が1なので7,11,13では割れません。
108のような2,8で終わる3桁の3の倍数の下に一つ違いの数を付けると13以下の素因数を持たない整数となり、素数の期待が高まります。その中で
・102101,102103
・108107,108109
・192191,192193
・312311,312313
・342341,342343
・522521,522523
・612611,612613
・822821,822823
・882881,882883
は双子素数です。闘会議をきっかけに調べてみました。
twitter.com本日のハイライト! 108109は素数でした!しかも108107も素数!覚えやすい上に双子素数!! #素数大富豪 #素数大富豪in闘会議 #闘会議2017 #闘会議 pic.twitter.com/LOlR4zNKpS
— 狡猾な狐@617伝道師 (@wreck1214) 2017年2月12日
17以上の倍数判定① ~3p法~
これは私が17以上の倍数判定をする際に最もよく使っている方法です。簡単に言うと「自然数nに素数pまたはその三倍(3p)を足すか引くかして一の位を0にする」方法で、以下の事実に基づいています。
つまり、pや3pを使えば一の位を0にできるのです。一の位の0は取って考えてよい(7以上の素数pについて、「10で割る」という操作は「pの倍数かどうか」には影響しない)ので、これで桁数を一つ減らせたことになります。
そして、桁を減らした後の数が2や5で割れるなら、一の位が1,3,7,9になるまで割りましょう。そうすれば再び3p法を適用できます。
例:1121から17*3=51を引くと1070であり、0を取った107は素数なので17で割れない。しかし1121に19を足すと1140であり、0を取った114は2で割ると57である。これは19*3である。よって1121は17の倍数ではないが19の倍数である。
17以上の倍数判定② ~概数法~
これは、判定したい自然数nの上3桁くらいを見てpの倍数が思い浮かんだときに有効な方法です。3p法に比べると自明なやり方ですが、うまく使い分けるとスピードが上がります。3p法が「下の位から攻める」のに対して、概数法は「上の位から攻める」方法です。
例:1021は4桁の数だが、上3桁を見ると102であり、102は17の倍数である。よって1020が17の倍数であり、1を加えた1021は17の倍数ではない。
さて、紹介する倍数判定法は以上ですが、最後にここまでの内容を踏まえて、1187が素数であることを確かめる手順の一例を解説します。
- 1187の一の位は7なので、2,5では割れない。また桁和は1+1+8+7=17なので3の倍数でもない。(一の位チェック&桁和チェック)
- 1187から1001を引くと186であり、186から91を2回引くと4が残る。当然4は7や13では割れない。また186の偶数桁和は8、奇数桁和は1+6=7であり、8-7=1は11で割れない。(1001チェック→91&交代和チェック)
- 1187から17を引くと1170であり、0を取った117から再び17を引くと100なので17では割れない。また1187から19*3=57を引くと1130であり、0を取った113は素数なので19で割れない。(3p法)
- 115は23の倍数、116は29の倍数である。1187-1150=37は23で割れず、1187-1160=27は29で割れない。(概数法)
- 1187に31*3=93を足すと1280であり、これは見るからに2,5以外の素因数を持たず31で割れない。(3p法)
37^2>35^2=1225>1187なので、ここまでで1187が素数だと分かったことになります。
なお、17以上の素数の倍数判定については、29など簡明な方法が見つかっているものもあります。
これらを併用できればより効率よく素数判定を進められるかもしれません。
それでは今日はこの辺で。